그래프 알고리즘으로, 문제를 풀 때 상당히 많이 사용한다.
경로를 찾는 문제 시, 상황에 맞게 DFS와 BFS를 활용하게 된다.
1. DFS
1.1 개념
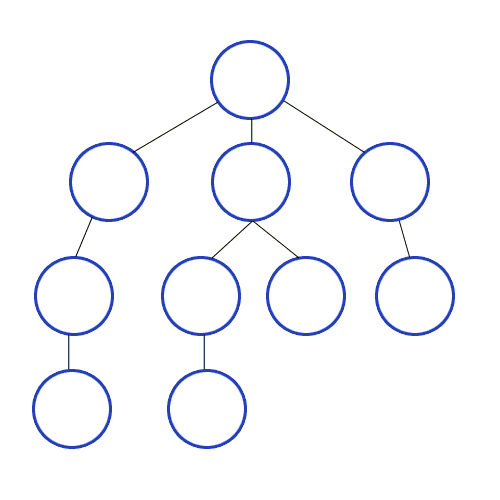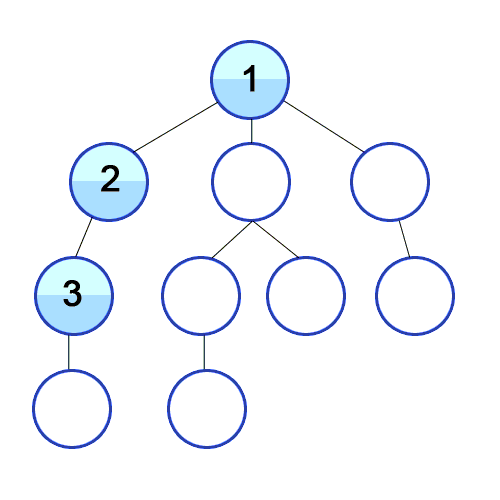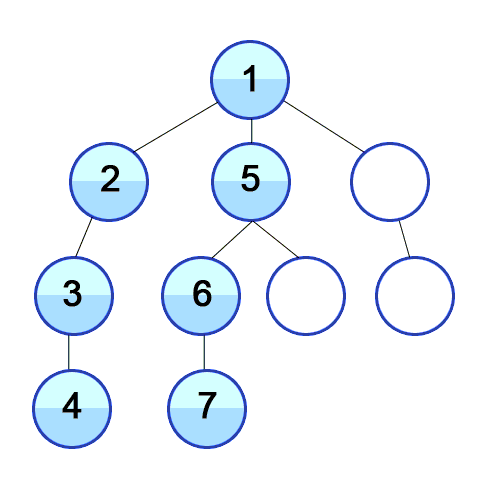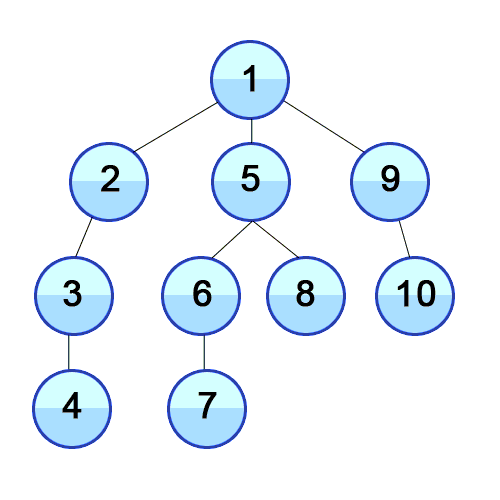
- 깊이 우선 탐색이며 DFS(Depth-First Search)라고 부른다.
- 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.
- 재귀함수를 통해 구현한다.(스택 자료구조를 이용하는 알고리즘이기 때문)
- 모든 경로를 방문해야 할 경우 사용에 적합하다.
- 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
- 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
1.2. 시간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(V+E)
- V는 접점, E는 간선을 뜻한다
1.3. Code
import java.io.*;
import java.util.*;
/**
* created by victory_woo on 02/04/2019
* DFS와 BFS 복습
*/
public class BOJ1260_RE {
private static final String SPACE = " ";
private static ArrayList<Integer>[] a;
private static boolean[] visit;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(SPACE);
int n = convert(input[0]); // 정점의 개수
int m = convert(input[1]); // 간선의 개수
int start = convert(input[2]); // 시작할 정점 번호
// 배열 초기화.
a = new ArrayList[n + 1];
visit = new boolean[n + 1];
for (int i = 1; i <= n; i++) {
a[i] = new ArrayList<>();
}
for (int j = 0; j < m; j++) {
String[] inputs = br.readLine().split(SPACE);
int u = convert(inputs[0]);
int v = convert(inputs[1]);
// 양방향 그래프일 경우 양쪽 다 추가해준다.
a[u].add(v);
a[v].add(u);
}
// 방문할 정점이 여러 개인 경우 정점 번호가 가장 작은 것부터 탐색하기 위해서 정렬한다.
for (int i = 1; i <= n; i++) {
Collections.sort(a[i]);
}
dfs(start);
}
private static int convert(String command) {
return Integer.parseInt(command);
}
private static void dfs(int x) {
// 방문한 적이 있다면 종료한다.
if (visit[x]) {
return;
}
visit[x] = true;
// 방문한 순서 출력
System.out.print(x+" ");
for (int y : a[x]) {
if (!visit[y]) {
dfs(y);
}
}
}
}
// 입력
5 4 5
5 4
4 3
4 2
1 5
// 출력 결과
5 1 4 2 3
// 입력
5 5 3
5 4
5 2
1 2
3 4
3 1
// 출력 결과
3 1 2 5 42. BFS
2.1. 개념
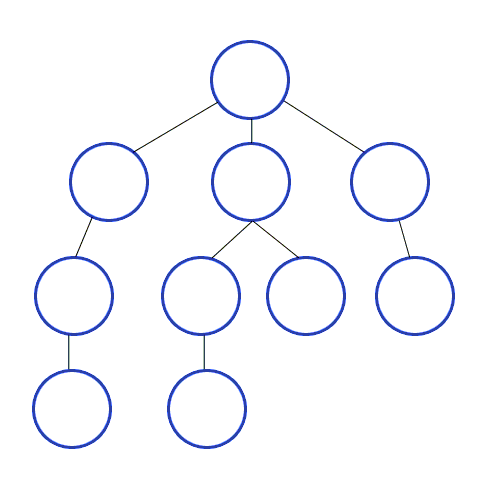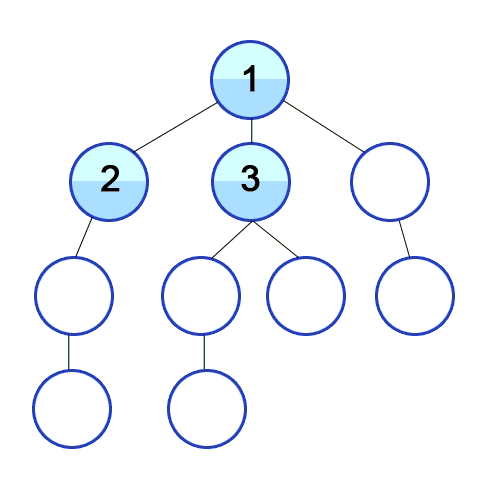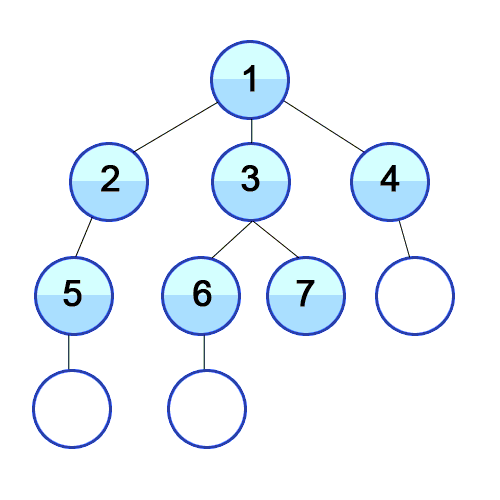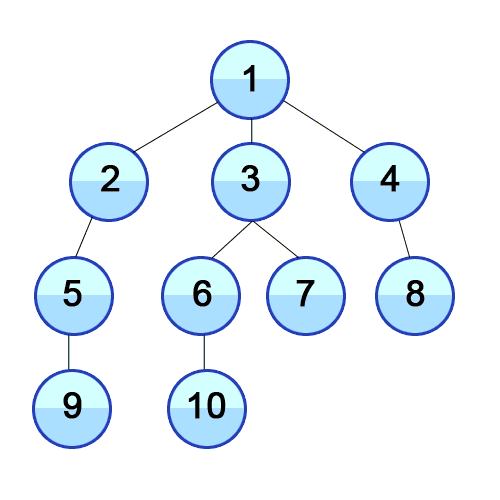
- 너비 우선 탐색이라 하며 BFS(Breadth-First Search)라 부른다.
- 루트 노드 혹은 임의의 노드에서 시작해 인접한 노드를 먼저 탐색하는 방법이다.
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법이다.
- 최대한 멀리 있는 노드를 우선으로 탐색하는 DFS와 반대다.
- 즉, 깊게 탐색하기 전에 넓게 탐색하는 것이다.
- 선입선출 방식인 큐를 사용한다. (해당 노드의 주변부터 탐색해야 하기 때문이다.)
- 최소 비용(즉, 모든 곳을 탐색하는 것보다 최소 비용이 우선일 때)에 적합하다.
- 두 노드 사이의 최단 경로(거리 1일 때) 혹은 임의의 경로를 찾고 싶을 때 이 방법을 선택한다.
- 이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
- 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
2.2. 시간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(V+E)
2.3. Code
import java.io.*;
import java.util.*;
public class Main {
private static final String SPACE = " ";
private static ArrayList<Integer>[] a;
private static boolean[] visit;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] input = br.readLine().split(SPACE);
int n = convert(input[0]); // 정점의 개수
int m = convert(input[1]); // 간선의 개수
int start = convert(input[2]); // 시작할 정점 번호
// 배열 초기화.
a = new ArrayList[n + 1];
for (int i = 1; i <= n; i++) {
a[i] = new ArrayList<>();
}
for (int j = 0; j < m; j++) {
String[] inputs = br.readLine().split(SPACE);
int u = convert(inputs[0]);
int v = convert(inputs[1]);
// 양방향 그래프일 경우 양쪽 다 추가해준다.
a[u].add(v);
a[v].add(u);
}
// 방문할 정점이 여러 개인 경우 정점 번호가 가장 작은 것부터 탐색하기 위해서 정렬한다.
for (int i = 1; i <= n; i++) {
Collections.sort(a[i]);
}
visit = new boolean[n + 1];
bfs(start);
System.out.println();
}
private static int convert(String command) {
return Integer.parseInt(command);
}
private static void bfs(int start) {
LinkedList<Integer> queue = new LinkedList<>();
visit[start] = true;
queue.add(start);
while (!queue.isEmpty()) {
int x = queue.remove(); // 큐에서 정점을 뺀다.
System.out.print(x + SPACE);
for (int y : a[x]) {
// 방문한 적이 있는지 체크한다.
if (!visit[y]) {
// 해당 정점을 방문한 적이 없다면 방문했다고 true 로 체크한다.
// 그리고 해당 정점을 큐에 넣는다.
visit[y] = true;
queue.add(y);
}
}
}
}
}
// 입력
5 5 3
5 4
5 2
1 2
3 4
3 1
// 출력 결과
3 1 4 2 5
참고
나동빈.『이것이 코딩테스트다 with 파이썬』.한빛미디어, 2020.
GitHub - WeareSoft/tech-interview: 🙍 tech interview
:loudspeaker:🙍 tech interview. Contribute to WeareSoft/tech-interview development by creating an account on GitHub.
github.com
https://gyoogle.dev/blog/algorithm/DFS%20&%20BFS.html
DFS & BFS | 👨🏻💻 Tech Interview
DFS & BFS 그래프 알고리즘으로, 문제를 풀 때 상당히 많이 사용한다. 경로를 찾는 문제 시, 상황에 맞게 DFS와 BFS를 활용하게 된다. DFS 루트 노드 혹은 임의 노드에서 다음 브랜치로 넘어가기 전에,
gyoogle.dev
https://github.com/WooVictory/Ready-For-Tech-Interview/blob/master/Algorithm/BFS%20%26%20DFS.md
GitHub - WooVictory/Ready-For-Tech-Interview: 💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간
💻 신입 개발자로서 준비를 하기 위해 지식을 정리하는 공간 👨💻. Contribute to WooVictory/Ready-For-Tech-Interview development by creating an account on GitHub.
github.com
'알고리즘' 카테고리의 다른 글
| MST(Minimum Spanning Tree) (0) | 2022.11.29 |
|---|---|
| 최단 경로 알고리즘 (0) | 2022.11.29 |
| DP(Dynamic Programming) (0) | 2022.11.29 |
| 정렬 (0) | 2022.11.28 |
| 알고리즘 (0) | 2022.11.28 |